仿射变换 affine transform v = ( v x v y v z 0 ) T \mathbf{v}=(v_x\;v_y\;v_z\;0)^T v = ( v x v y v z 0 ) T v = ( v x v y v z 1 ) T \mathbf{v}=(v_x\;v_y\;v_z\;1)^T v = ( v x v y v z 1 ) T
所有的平移、旋转、缩放、反射和剪切矩阵都是仿射的。
一个点从一个坐标移动向量t = ( t x , t y , t z ) \mathbf{t}=(t_x,t_y,t_z) t = ( t x , t y , t z )
T ( t ) = T ( t x , t y , t z ) = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] \mathbf{T}(t)=\mathbf{T}(t_{x},t_{y},t_{z})=\begin{bmatrix}
1 & 0 & 0 & t_{x}\\
0 & 1 & 0 & t_{y}\\
0 & 0 & 1 & t_{z}\\
0 & 0 & 0 & 1
\end{bmatrix} T ( t ) = T ( t x , t y , t z ) = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 t x t y t z 1 ⎦ ⎥ ⎥ ⎥ ⎤
图中方块按照平移矩阵T ( 5 , 2 , 0 ) \mathbf{T}(5,2,0) T ( 5 , 2 , 0 )
明显可知,一个点p = ( p x p y p z 1 ) T \mathbf{p}=(p_x\;\;p_y\;\;p_z\;\;1)^T p = ( p x p y p z 1 ) T T ( t ) T(t) T ( t ) p ′ = ( p x + t x p y + t y p z + t z 1 ) T \mathbf{p{}'}=(p_x+t_x\;\;p_y+t_y\;\;p_z+t_z\;\;1)^T p ′ = ( p x + t x p y + t y p z + t z 1 ) T v = ( v x v y v z 0 ) T \mathbf{v}=(v_x\;\;v_y\;\;v_z\;\;0)^T v = ( v x v y v z 0 ) T T \mathbf{T} T
T ( t ) ∗ p = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] ∗ [ p x p y p z 1 ] = [ p x + t x p y + t y p z + t z 1 ] \mathbf{T}(t)*\mathbf{p}=\begin{bmatrix}
1 & 0 & 0 & t_{x}\\
0 & 1 & 0 & t_{y}\\
0 & 0 & 1 & t_{z}\\
0 & 0 & 0 & 1
\end{bmatrix}*\begin{bmatrix}
p_{x}\\
p_{y}\\
p_{z}\\
1
\end{bmatrix}=\begin{bmatrix}
p_{x}+t_{x}\\
p_{y}+t_{y}\\
p_{z}+t_{z}\\
1
\end{bmatrix} T ( t ) ∗ p = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 t x t y t z 1 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ p x p y p z 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ p x + t x p y + t y p z + t z 1 ⎦ ⎥ ⎥ ⎥ ⎤
T ( t ) ∗ v = [ 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ] ∗ [ v x v y v z 0 ] = [ v x v y v z 0 ] \mathbf{T}(t)*\mathbf{v}=\begin{bmatrix}
1 & 0 & 0 & t_{x}\\
0 & 1 & 0 & t_{y}\\
0 & 0 & 1 & t_{z}\\
0 & 0 & 0 & 1
\end{bmatrix}*\begin{bmatrix}
v_{x}\\
v_{y}\\
v_{z}\\
0
\end{bmatrix}=\begin{bmatrix}
v_{x}\\
v_{y}\\
v_{z}\\
0
\end{bmatrix} T ( t ) ∗ v = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 t x t y t z 1 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ v x v y v z 0 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ v x v y v z 0 ⎦ ⎥ ⎥ ⎥ ⎤
平移矩阵的逆矩阵为T − 1 ( t ) = T ( − t ) \mathbf{T}^{-1}(t)=\mathbf{T}(-t) T − 1 ( t ) = T ( − t )
逆矩阵:给定一个n ∗ n n*n n ∗ n A \mathbf{A} A B \mathbf{B} B A B = B A = I n \mathbf{AB}=\mathbf{BA}=\mathbf{I}_n A B = B A = I n A \mathbf{A} A B \mathbf{B} B A \mathbf{A} A A − 1 \mathbf{A}^{-1} A − 1 I n \mathbf{I}_n I n [ 1 0 0 . . . 0 1 0 . . . 0 0 1 . . . . . . . . . . . . 1 ] \begin{bmatrix}1 & 0 & 0 & ...\\0 & 1 & 0 & ...\\0 & 0 & 1 & ...\\... & ... & ... & 1\end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 . . . 0 1 0 . . . 0 0 1 . . . . . . . . . . . . 1 ⎦ ⎥ ⎥ ⎥ ⎤
在二维中,旋转矩阵很容易推导。假设现在有一个向量v = ( v x , v y ) \mathbf{v}=(v_x,v_y) v = ( v x , v y ) v = ( v x , v y ) = ( r c o s θ , r s i n θ ) \mathbf{v}=(v_x,v_y)=(rcos\theta,rsin\theta) v = ( v x , v y ) = ( r c o s θ , r s i n θ ) ϕ ∘ \phi^{\circ} ϕ ∘ u = ( r c o s ( θ + ϕ ) , r s i n ( θ + ϕ ) ) \mathbf{u}=(rcos(\theta+\phi),rsin(\theta+\phi)) u = ( r c o s ( θ + ϕ ) , r s i n ( θ + ϕ ) )
u = [ r cos ( θ + ϕ ) r sin ( θ + ϕ ) ] = [ r ( cos θ cos ϕ − sin θ sin ϕ ) r ( sin θ cos ϕ − cos θ sin ϕ ) ] = [ cos ϕ − sin ϕ sin ϕ cos ϕ ] ⏟ R ( ϕ ) [ r cos θ r sin θ ] ⏟ v = R ( ϕ ) v \mathbf{u}=\begin{bmatrix}
r\cos(\theta + \phi )\\
r\sin(\theta + \phi )
\end{bmatrix}=\begin{bmatrix}
r(\cos\theta \cos\phi -\sin\theta \sin\phi)\\
r(\sin\theta \cos\phi -\cos\theta \sin\phi)
\end{bmatrix}\\
=\underbrace{\begin{bmatrix}
\cos\phi& -\sin\phi\\
\sin\phi & \cos\phi
\end{bmatrix}}_{\mathbf{R}(\phi)}\underbrace{\begin{bmatrix}
r\cos\theta\\
r\sin\theta
\end{bmatrix}}_{\mathbf{v}}=\mathbf{R}(\phi)\mathbf{v} u = [ r cos ( θ + ϕ ) r sin ( θ + ϕ ) ] = [ r ( cos θ cos ϕ − sin θ sin ϕ ) r ( sin θ cos ϕ − cos θ sin ϕ ) ] = R ( ϕ ) [ cos ϕ sin ϕ − sin ϕ cos ϕ ] v [ r cos θ r sin θ ] = R ( ϕ ) v
在三维中,我们通常用R x ( ϕ ) \mathbf{R}_x(\phi) R x ( ϕ ) R y ( ϕ ) \mathbf{R}_y(\phi) R y ( ϕ ) R z ( ϕ ) \mathbf{R}_z(\phi) R z ( ϕ ) ϕ ∘ \phi^{\circ} ϕ ∘
R x ( ϕ ) = [ 1 0 0 0 0 cos ϕ − sin ϕ 0 0 sin ϕ cos ϕ 0 0 0 0 1 ] \mathbf{R}_{x}(\phi)=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & \cos\phi & -\sin\phi & 0\\
0 & \sin\phi & \cos\phi & 0\\
0 & 0 & 0 & 1
\end{bmatrix} R x ( ϕ ) = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 cos ϕ sin ϕ 0 0 − sin ϕ cos ϕ 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
R y ( ϕ ) = [ cos ϕ 0 sin ϕ 0 0 1 0 0 − sin ϕ 0 cos ϕ 0 0 0 0 1 ] \mathbf{R}_{y}(\phi)=\begin{bmatrix}
\cos\phi & 0 & \sin\phi & 0\\
0 & 1 & 0 & 0\\
-\sin\phi & 0 & \cos\phi & 0\\
0 & 0 & 0 & 1
\end{bmatrix} R y ( ϕ ) = ⎣ ⎢ ⎢ ⎢ ⎡ cos ϕ 0 − sin ϕ 0 0 1 0 0 sin ϕ 0 cos ϕ 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
R z ( ϕ ) = [ cos ϕ − sin ϕ 0 0 sin ϕ cos ϕ 0 0 0 0 1 0 0 0 0 1 ] \mathbf{R}_{z}(\phi)=\begin{bmatrix}
\cos\phi & -\sin\phi & 0 & 0\\
\sin\phi & \cos\phi & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} R z ( ϕ ) = ⎣ ⎢ ⎢ ⎢ ⎡ cos ϕ sin ϕ 0 0 − sin ϕ cos ϕ 0 0 0 0 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
如果将上述4x4的矩阵的最下行和最右列删除,就会得到一个3x3矩阵。这样的3x3矩阵R 表示沿着任意轴旋转ϕ ∘ \phi^{\circ} ϕ ∘ 迹 Trace n ∗ n n*n n ∗ n
t r ( R ) = 1 + 2 cos ϕ tr(\mathbf{R})=1+2\cos\phi t r ( R ) = 1 + 2 cos ϕ
R i ( ϕ ) \mathbf{R}_i(\phi) R i ( ϕ ) ϕ ∘ \phi^{\circ} ϕ ∘
所有旋转矩阵的行列式 determinant 正交矩阵 orthogonal matrix
行列式:二维矩阵d e t ( A ) = ∥ A ∣ = d e t ( [ a b c d ] ) = a d − b c det(\mathbf{A})=\|\mathbf{A}| =det(\begin{bmatrix}a & b\\c & d\end{bmatrix})=ad-bc d e t ( A ) = ∥ A ∣ = d e t ( [ a c b d ] ) = a d − b c
转置矩阵:矩阵A \mathbf{A} A A T \mathbf{A}^T A T A \mathbf{A} A A T \mathbf{A}^T A T A \mathbf{A} A A T \mathbf{A}^T A T [ 1 2 3 4 5 6 ] T = [ 1 3 5 2 4 6 ] \begin{bmatrix}1 & 2\\ 3 & 4\\ 5 & 6\end{bmatrix}^T=\begin{bmatrix}1 & 3 & 5\\ 2 & 4 & 6\end{bmatrix} ⎣ ⎢ ⎡ 1 3 5 2 4 6 ⎦ ⎥ ⎤ T = [ 1 2 3 4 5 6 ]
正交矩阵:矩阵Q \mathbf{Q} Q Q T \mathbf{Q}^T Q T Q − 1 \mathbf{Q}^{-1} Q − 1
∵ 1 = d e t ( I ) = d e t ( Q − 1 Q ) = d e t ( Q T Q ) = d e t ( Q T ) ∗ d e t ( Q ) = ( d e t ( Q ) ) 2 \because 1=det(I)=det(Q^{-1}Q)=det(Q^TQ)=det(Q^T)*det(Q)=(det(Q))^2 ∵ 1 = d e t ( I ) = d e t ( Q − 1 Q ) = d e t ( Q T Q ) = d e t ( Q T ) ∗ d e t ( Q ) = ( d e t ( Q ) ) 2
∴ d e t ( Q ) = ± 1 \therefore det(Q)=\pm 1 ∴ d e t ( Q ) = ± 1
现在假设我们要将一个物体沿z轴旋转ϕ ∘ \phi^{\circ} ϕ ∘ p 。首先,我们要先将物体按照T ( − p ) \mathbf{T}(-p) T ( − p ) p 点在原点,不受旋转影响。接着,对物体按照R z ( ϕ ) \mathbf{R}_z(\phi) R z ( ϕ ) T ( p ) \mathbf{T}(p) T ( p )
X = T ( p ) R z ( ϕ ) T ( − p ) \mathbf{X}=\mathbf{T}(\mathbf{p})\mathbf{R}_z(\phi)\mathbf{T}(\mathbf{-p})
X = T ( p ) R z ( ϕ ) T ( − p )
缩放矩阵用S ( s ) = S ( s x , s y , s z ) \mathbf{S}(s)=\mathbf{S}(s_x,s_y,s_z) S ( s ) = S ( s x , s y , s z ) s x s_x s x s y s_y s y s z s_z s z
S ( s ) = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] \mathbf{S}(s)=\begin{bmatrix}
s_x & 0 & 0 &0\\
0 & s_y & 0 &0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & 1
\end{bmatrix} S ( s ) = ⎣ ⎢ ⎢ ⎢ ⎡ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
如果s x = s y = s z s_x=s_y=s_z s x = s y = s z 均匀 uniform 各向同性 isotropic 不均匀 nonuniform 各向异性 anisotropic S − 1 ( s ) = S ( 1 / s x , 1 / s y , 1 / s z ) \mathbf{S}^{-1}(s)=\mathbf{S}(1/s_x,1/s_y,1/s_z) S − 1 ( s ) = S ( 1 / s x , 1 / s y , 1 / s z )
当使用齐次坐标时,可以通过修改矩阵最右下角的值来表示缩放。假设我们要将一个物体放大5倍,可以用两种方式来表示:
S = [ 5 0 0 0 0 5 0 0 0 0 5 0 0 0 0 1 ] , S ′ = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 / 5 ] \mathbf{S}=\begin{bmatrix}
5 & 0 & 0 &0\\
0 & 5 & 0 &0\\
0 & 0 & 5 & 0\\
0 & 0 & 0 & 1
\end{bmatrix},\;\;\;\;\;\;\mathbf{S}{}'=\begin{bmatrix}
1 & 0 & 0 &0\\
0 & 1 & 0 &0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1/5
\end{bmatrix} S = ⎣ ⎢ ⎢ ⎢ ⎡ 5 0 0 0 0 5 0 0 0 0 5 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ , S ′ = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 / 5 ⎦ ⎥ ⎥ ⎥ ⎤
前者可以用来进行不均匀缩放,而后者只能进行均匀缩放。由于后者涉及到齐次坐标的除法,效率可能会降低,除非系统不管右下角的数值是否是1都会进行一次除法计算。
如果s 向量中有某个值是负值,则该矩阵为反射矩阵 reflection matrix 镜像矩阵 mirror matrix
反射矩阵通常需要特殊处理。例如,一个三角形三个顶点的顺序是逆时针的,在经过反射矩阵变换后,就变成了顺时针的,如果不处理,就会导致光照和背向剔除出现问题。我们可以通过计算4x4矩阵的左上角3x3区域的矩阵的行列式来判断原矩阵是否是反射矩阵,如果行列式为负数,则说明它是反射矩阵。
剪切矩阵可以用来扭曲整个场景或模型外观。它一共有6种基本矩阵,分别表示为H x y ( s ) , H x z ( s ) , H y x ( s ) , H y z ( s ) , H z x ( s ) , H z y ( s ) \mathbf{H}_{xy}(s),\mathbf{H}_{xz}(s),\mathbf{H}_{yx}(s),\mathbf{H}_{yz}(s),\mathbf{H}_{zx}(s),\mathbf{H}_{zy}(s) H x y ( s ) , H x z ( s ) , H y x ( s ) , H y z ( s ) , H z x ( s ) , H z y ( s )
H x z ( s ) = [ 1 0 s 0 0 1 0 0 0 0 1 0 0 0 0 1 ] \mathbf{H}_{xz}(s)=\begin{bmatrix}
1 & 0 & s & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} H x z ( s ) = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 s 0 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
一个点p = ( p x p y p z 1 ) T \mathbf{p}=(p_x\;\;p_y\;\;p_z\;\;1)^T p = ( p x p y p z 1 ) T p ′ = ( p x + s p z p y p z 1 ) T \mathbf{p{}'}=(p_x+sp_z\;\;p_y\;\;p_z\;\;1)^T p ′ = ( p x + s p z p y p z 1 ) T
H x z ( s ) ∗ p = [ 1 0 s 0 0 1 0 0 0 0 1 0 0 0 0 1 ] ∗ [ p x p y p z 1 ] = [ p x + s p z p y p z 1 ] \mathbf{H}_{xz}(s)*\mathbf{p}=\begin{bmatrix}
1 & 0 & s &0\\
0 & 1 & 0 &0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}*\begin{bmatrix}
p_x\\
p_y\\
p_z\\
1\end{bmatrix}=\begin{bmatrix}
p_x+sp_z\\
p_y\\
p_z\\
1\end{bmatrix} H x z ( s ) ∗ p = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 s 0 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ p x p y p z 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ p x + s p z p y p z 1 ⎦ ⎥ ⎥ ⎥ ⎤
其结果如下图所示:
剪切矩阵的逆矩阵为H i j − 1 ( s ) = H i j ( − s ) \mathbf{H}_{ij}^{-1}(s)=\mathbf{H}_{ij}(-s) H i j − 1 ( s ) = H i j ( − s )
剪切矩阵还有另外一种表现方式是:
H x y ′ ( s , t ) = [ 1 0 s 0 0 1 t 0 0 0 1 0 0 0 0 1 ] \mathbf{H}_{xy}{}'(s,t)=\begin{bmatrix}
1 & 0 & s &0\\
0 & 1 & t &0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} H x y ′ ( s , t ) = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 s t 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
在这种情况下,两个下标的轴向都会发生变换,另外一个轴的值将作为变换的系数
H x y ′ ( s , t ) ∗ p = [ 1 0 s 0 0 1 t 0 0 0 1 0 0 0 0 1 ] ∗ [ p x p y p z 1 ] = [ p x + s p z p y + t p z p z 1 ] \mathbf{H}_{xy}{}'(s,t)*\mathbf{p}=\begin{bmatrix}
1 & 0 & s &0\\
0 & 1 & t &0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix}*\begin{bmatrix}
p_x\\
p_y\\
p_z\\
1\end{bmatrix}=\begin{bmatrix}
p_x+sp_z\\
p_y+tp_z\\
p_z\\
1\end{bmatrix} H x y ′ ( s , t ) ∗ p = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 s t 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ ∗ ⎣ ⎢ ⎢ ⎢ ⎡ p x p y p z 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ p x + s p z p y + t p z p z 1 ⎦ ⎥ ⎥ ⎥ ⎤
需要注意的是,所有剪切矩阵的行列式都为1,不会改变物体体积。
由于矩阵在乘法运算上的非互换性,变换的级联是和顺序相关的。如下图所示,先旋转再缩放和先缩放再旋转得到的结果完全不同。
将一系列变换矩阵级联成一个矩阵可以提高效率。这个单一矩阵为C = T R S \mathbf{C}=\mathbf{TRS} C = T R S C p = T R S p = T ( R ( S p ) ) \mathbf{Cp}=\mathbf{TRSp}=\mathbf{T(R(Sp))} C p = T R S p = T ( R ( S p ) )
另外需要注意的是,在遵从上述乘法运算顺序的前提下,TRSp 可以被自行组合。比如,可以将其组合成(TR )(Sp )。
对于一个坚硬的物体来说,它的变换过程只有位置和角度会发生变化,形状不会发生变化。这种只包含位移和旋转矩阵的变换叫做Rigid-Body Transform,可以表示为:
X = T ( t ) R = [ r 00 r 01 r 02 t x r 10 r 11 r 12 t y r 20 r 21 r 22 t z 0 0 0 1 ] \mathbf{X}=\mathbf{T}(t)\mathbf{R}=\begin{bmatrix}
r_{00} & r_{01} & r_{02} & t_x\\
r_{10} & r_{11} & r_{12} & t_y\\
r_{20} & r_{21} & r_{22} & t_z\\
0 & 0 & 0 & 1\\
\end{bmatrix} X = T ( t ) R = ⎣ ⎢ ⎢ ⎢ ⎡ r 0 0 r 1 0 r 2 0 0 r 0 1 r 1 1 r 2 1 0 r 0 2 r 1 2 r 2 2 0 t x t y t z 1 ⎦ ⎥ ⎥ ⎥ ⎤
它的逆矩阵为X − 1 = ( T ( t ) R ) − 1 = R − 1 T − 1 ( t ) = R T T ( − t ) \mathbf{X}^{-1}=(\mathbf{T}(t)\mathbf{R})^{-1}=\mathbf{R}^{-1}\mathbf{T}^{-1}(t)=\mathbf{R}^T\mathbf{T}(-t) X − 1 = ( T ( t ) R ) − 1 = R − 1 T − 1 ( t ) = R T T ( − t ) R T
假设我们要和OpenGL Utility Library GLU c \mathbf{c} c l \mathbf{l} l u ′ \mathbf{u}{}' u ′ r , u , v \mathbf{r,u,v} r , u , v
首先计算视角向量(view vector),v = ( c − l ) / ∥ c − l ∥ \mathbf{v}=(\mathbf{c}-\mathbf{l})/\| \mathbf{c}-\mathbf{l}\| v = ( c − l ) / ∥ c − l ∥ u ′ \mathbf{u}{}' u ′ v \mathbf{v} v r = − ( v × u ′ ) / ∥ v × u ′ ∥ \mathbf{r}=-(\mathbf{v}\times \mathbf{u}{}')/\| \mathbf{v}\times \mathbf{u}{}'\| r = − ( v × u ′ ) / ∥ v × u ′ ∥ u ′ \mathbf{u}{}' u ′ u = v × r \mathbf{u}=\mathbf{v}\times \mathbf{r} u = v × r
在构建相机的变换矩阵M \mathbf{M} M r , u , v \mathbf{r,u,v} r , u , v T(t)R
M = ( T ( t ) R ) − 1 = R − 1 T − 1 ( t ) \mathbf{M}=(\mathbf{T}(t)\mathbf{R})^{-1}=\mathbf{R}^{-1}\mathbf{T}^{-1}(t)
M = ( T ( t ) R ) − 1 = R − 1 T − 1 ( t )
我们知道,一个矩阵[ x x y x z x x y y y z y x z y z z z ] \begin{bmatrix}x_x & y_x & z_x\\x_y & y_y & z_y\\x_z & y_z & z_z\end{bmatrix} ⎣ ⎢ ⎡ x x x y x z y x y y y z z x z y z z ⎦ ⎥ ⎤ ( x x , x y , x z ⃗ ) (\vec{x_x,x_y,x_z}) ( x x , x y , x z ) ( y x , y y , y z ⃗ ) (\vec{y_x,y_y,y_z}) ( y x , y y , y z ) ( z x , z y , z z ⃗ ) (\vec{z_x,z_y,z_z}) ( z x , z y , z z )
M = [ r x u x v x 0 r y u y v y 0 r z u z v z 0 0 0 0 1 ] − 1 T − 1 ( t ) \mathbf{M}=\begin{bmatrix}r_x & u_x & v_x & 0\\r_y & u_y & v_y & 0\\r_z & u_z & v_z & 0\\0 & 0 & 0 & 1\end{bmatrix}^{-1}T^{-1}(t)
M = ⎣ ⎢ ⎢ ⎢ ⎡ r x r y r z 0 u x u y u z 0 v x v y v z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ − 1 T − 1 ( t )
由于r , u , v r,u,v r , u , v
M = [ r x r y r z 0 u x u y u z 0 v x v y v z 0 0 0 0 1 ] T ( − t ) = [ r x r y r z 0 u x u y u z 0 v x v y v z 0 0 0 0 1 ] [ 1 0 0 − t x 0 1 0 − t y 0 0 1 − t z 0 0 0 1 ] = [ r x r y r z − ( r x t x + r y t y + r z t z ) u x u y u z − ( u x t x + u y t y + u z t z ) v x v y v z − ( v x t x + v y t y + v z t z ) 0 0 0 1 ] = [ r x r y r z − t ⋅ r u x u y u z − t ⋅ u v x v y v z − t ⋅ v 0 0 0 1 ] \mathbf{M}=\begin{bmatrix}r_x & r_y & r_z & 0\\u_x & u_y & u_z & 0\\v_x & v_y & v_z & 0\\0 & 0 & 0 & 1\end{bmatrix}\mathbf{T}(-\mathbf{t})=\begin{bmatrix}r_x & r_y & r_z & 0\\u_x & u_y & u_z & 0\\v_x & v_y & v_z & 0\\0 & 0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0 & -t_x\\0 & 1 & 0 & -t_y\\0 & 0 & 1 & -t_z\\0 & 0 & 0 & 1\end{bmatrix}\\=\begin{bmatrix}r_x & r_y & r_z & -(r_xt_x+r_yt_y+r_zt_z)\\u_x & u_y & u_z & -(u_xt_x+u_yt_y+u_zt_z)\\v_x & v_y & v_z & -(v_xt_x+v_yt_y+v_zt_z)\\0 & 0 & 0 & 1\end{bmatrix}=\begin{bmatrix}r_x & r_y & r_z & -\mathbf{t}\cdot \mathbf{r}\\u_x & u_y & u_z & -\mathbf{t}\cdot \mathbf{u}\\v_x & v_y & v_z & -\mathbf{t}\cdot \mathbf{v}\\0 & 0 & 0 & 1\end{bmatrix}
M = ⎣ ⎢ ⎢ ⎢ ⎡ r x u x v x 0 r y u y v y 0 r z u z v z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ T ( − t ) = ⎣ ⎢ ⎢ ⎢ ⎡ r x u x v x 0 r y u y v y 0 r z u z v z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 − t x − t y − t z 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ r x u x v x 0 r y u y v y 0 r z u z v z 0 − ( r x t x + r y t y + r z t z ) − ( u x t x + u y t y + u z t z ) − ( v x t x + v y t y + v z t z ) 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ r x u x v x 0 r y u y v y 0 r z u z v z 0 − t ⋅ r − t ⋅ u − t ⋅ v 1 ⎦ ⎥ ⎥ ⎥ ⎤
本章中提到的转换矩阵都不适用于法线,下图就是将缩放矩阵应用于法线的错误例子:
正确的计算方式是乘以矩阵的伴随矩阵 adjoint
伴随矩阵:A \mathbf{A} A a d j ( A ) adj(\mathbf{A}) a d j ( A ) A ∗ \mathbf{A}^* A ∗ A \mathbf{A} A A ∗ = A − 1 ∗ d e t ( A ) \mathbf{A}^*=\mathbf{A}^{-1}*det(\mathbf{A}) A ∗ = A − 1 ∗ d e t ( A )
计算一个4x4矩阵的伴随矩阵的性能开销很大也没必要。位移并不会改变法线向量,而且大多数模型变换都是仿射的,并不会进行投影改变齐次坐标的w分量。因此在大多数情况下,都只需要计算左上角3x3矩阵的伴随矩阵即可。
通常甚至连伴随矩阵都不需要计算。假设一个变换矩阵只包含了位移、旋转和统一缩放。其中位移不会影响法线向量,统一缩放只会改变法线向量的长度,而旋转也只是改变了一个角度而已。传统的计算法线变换的方式就是求取变换矩阵的逆矩阵的转置矩阵,而旋转矩阵的逆矩阵和转置矩阵相等,它的逆矩阵的转置矩阵就是它自己。因此在这种情况下,模型的变换矩阵就能用来计算法线变换矩阵。
最后,normalize也并不是每次都需要执行的。假如变换只包含了位移和旋转,那法线向量的长度并没有被改变,因此不需要normalize。如果是统一缩放,那归一化时也只需要除以缩放系数就行,或者在计算时先将变换矩阵左上角3x3的部分除以缩放系数。
下面三种方法可以计算逆矩阵:
如果由一个或一组简单变换组成的变换矩阵,则将其系数取负、顺序颠倒即可。如M = T ( t ) R ( ϕ ) \mathbf{M}=\mathbf{T}(\mathbf{t})\mathbf{R}(\phi) M = T ( t ) R ( ϕ ) M − 1 = R ( − ϕ ) T ( − t ) \mathbf{M}^{-1}=\mathbf{R}(-\phi)\mathbf{T}(\mathbf{-t}) M − 1 = R ( − ϕ ) T ( − t )
如果矩阵是正交矩阵,则逆矩阵为转置矩阵。一个或一组旋转矩阵都是正交矩阵。
如果不确定,则使用伴随矩阵、克莱默法则 Cramer’s Rule LU 分解 LU Decomposition 高斯消元法 Gaussian elimination
克莱默法则:详细的推导和几何理解可以参考该视频 。结论是:
如果A = [ a b c d ] , A ⋅ [ x y ] = [ 1 2 ] \mathbf{A}=\begin{bmatrix}a & b\\c & d\end{bmatrix},\mathbf{A}\cdot \begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}1\\2\end{bmatrix} A = [ a c b d ] , A ⋅ [ x y ] = [ 1 2 ]
则x = d e t ( [ 1 b 2 d ] ) d e t ( A ) , y = d e t ( [ a 1 c 2 ] ) d e t ( A ) x=\frac{det(\begin{bmatrix}1 & b\\ 2 & d\end{bmatrix})}{det(\mathbf{A})},y=\frac{det(\begin{bmatrix}a & 1\\ c & 2\end{bmatrix})}{det(\mathbf{A})} x = d e t ( A ) d e t ( [ 1 2 b d ] ) , y = d e t ( A ) d e t ( [ a c 1 2 ] )
对于逆矩阵,我们知道A A − 1 = I \mathbf{A}\mathbf{A}^{-1}=\mathbf{I} A A − 1 = I
假设A = [ a b c d ] , A − 1 = [ x 1 x 2 y 1 y 2 ] \mathbf{A}=\begin{bmatrix}a & b\\c & d\end{bmatrix},\mathbf{A}^{-1}=\begin{bmatrix}x_1 & x_2\\y_1 & y_2\end{bmatrix} A = [ a c b d ] , A − 1 = [ x 1 y 1 x 2 y 2 ]
则有:[ a b c d ] [ x 1 x 2 ] = [ 1 0 ] , [ a b c d ] [ y 1 y 2 ] = [ 0 1 ] \begin{bmatrix}a & b\\c & d\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}1\\0\end{bmatrix},\begin{bmatrix}a & b\\c & d\end{bmatrix}\begin{bmatrix}y_1\\y_2\end{bmatrix}=\begin{bmatrix}0\\1\end{bmatrix} [ a c b d ] [ x 1 x 2 ] = [ 1 0 ] , [ a c b d ] [ y 1 y 2 ] = [ 0 1 ]
根据克莱默法则可得: x 1 = d d e t ( A ) , x 2 = − c d e t ( A ) , y 1 = − b d e t ( A ) , y 2 = a d e t ( A ) x_1=\frac{d}{det(\mathbf{A})},x_2=\frac{-c}{det(\mathbf{A})},y_1=\frac{-b}{det(\mathbf{A})},y_2=\frac{a}{det(\mathbf{A})} x 1 = d e t ( A ) d , x 2 = d e t ( A ) − c , y 1 = d e t ( A ) − b , y 2 = d e t ( A ) a
因此:A − 1 = 1 d e t ( A ) [ d − b − c a ] \mathbf{A}^{-1}=\frac{1}{det(\mathbf{A})}\begin{bmatrix}d & -b\\-c & a\end{bmatrix} A − 1 = d e t ( A ) 1 [ d − c − b a ]
这个变换用来改变物体的朝向。
用来转换物体的朝向,其矩阵可以有很多种顺序组合,但通常表示为:
E ( h , p , r ) = R z ( r ) R x ( p ) R y ( h ) \mathbf{E}(h,p,r)=\mathbf{R}_z(r)\mathbf{R}_x(p)\mathbf{R}_y(h)
E ( h , p , r ) = R z ( r ) R x ( p ) R y ( h )
由于E 是多个旋转矩阵的组合,因此它是正交矩阵。它的逆矩阵E − 1 = E T = ( R z R x R y ) T = R y T R x T R z T \mathbf{E}^{-1}=\mathbf{E}^{T}=(\mathbf{R}_z\mathbf{R}_x\mathbf{R}_y)^{T}=\mathbf{R}_y^{T}\mathbf{R}_x^{T}\mathbf{R}_z^{T} E − 1 = E T = ( R z R x R y ) T = R y T R x T R z T E 自己的转置矩阵。
欧拉角 Euler angles
不同的软件对于朝上的轴向定义不同,主要有z、-z、y轴朝向。本章节我们默认y轴朝向。
Euler angles适用于小角度转换或视角转向,但局限性也很大。比如,它很难处理两组E 的组合,因为在两组E 之间进行插值并不是简单的对h、p、r做插值,假设有两组完全不同的r、p、y,其实最后的结果E 完全相同,那它们之间的插值也应该都是E ,而如果对h、p、r做插值,得到的结果就不会和E 相同。
从E中推导出h、p、r三个值的过程如下(由于都是旋转矩阵,因此不需要使用4x4矩阵,只需要3x3矩阵):
E ( h , p , r ) = [ e 00 e 01 e 02 e 10 e 11 e 12 e 20 e 21 e 22 ] = R z ( r ) R x ( p ) R y ( h ) \mathbf{E}(h,p,r)=\begin{bmatrix}e_{00} & e_{01} & e_{02}\\e_{10} & e_{11} & e_{12}\\e_{20} & e_{21} & e_{22}\end{bmatrix}=\mathbf{R}_z(r)\mathbf{R}_x(p)\mathbf{R}_y(h)
E ( h , p , r ) = ⎣ ⎢ ⎡ e 0 0 e 1 0 e 2 0 e 0 1 e 1 1 e 2 1 e 0 2 e 1 2 e 2 2 ⎦ ⎥ ⎤ = R z ( r ) R x ( p ) R y ( h )
= [ cos r − sin r 0 sin r cos r 0 0 0 1 ] [ 1 0 0 0 c o s p − sin p 0 sin p cos p ] [ cos h 0 sin h 0 1 0 − sin h 0 cos h ] =\begin{bmatrix}\cos r & -\sin r & 0\\\sin r & \cos r & 0\\0 & 0 & 1\end{bmatrix}\begin{bmatrix}1 & 0 & 0\\0 & cos p & -\sin p\\0 & \sin p & \cos p\end{bmatrix}\begin{bmatrix}\cos h & 0 & \sin h\\0 & 1 & 0\\-\sin h & 0 & \cos h\end{bmatrix}
= ⎣ ⎢ ⎡ cos r sin r 0 − sin r cos r 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ 1 0 0 0 c o s p sin p 0 − sin p cos p ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ cos h 0 − sin h 0 1 0 sin h 0 cos h ⎦ ⎥ ⎤
= [ cos r − sin r 0 sin r cos r 0 0 0 1 ] [ cos h 0 sin h sin p sin h cos p − sin p cos h − cos p sin h sin p cos p cos h ] =\begin{bmatrix}\cos r & -\sin r & 0\\\sin r & \cos r & 0\\0 & 0 & 1\end{bmatrix}\begin{bmatrix}\cos h & 0 & \sin h\\\sin p\sin h & \cos p & -\sin p\cos h\\-\cos p\sin h & \sin p & \cos p\cos h\end{bmatrix}
= ⎣ ⎢ ⎡ cos r sin r 0 − sin r cos r 0 0 0 1 ⎦ ⎥ ⎤ ⎣ ⎢ ⎡ cos h sin p sin h − cos p sin h 0 cos p sin p sin h − sin p cos h cos p cos h ⎦ ⎥ ⎤
= [ cos r cos h − sin r sin p sin h − sin r cos p cos r sin h + sin r sin p cos h sin r cos h + cos r sin p sin h cos r cos p sin r sin h − cos r sin p cos h − cos p sin h sin p cos p cos h ] =\begin{bmatrix}\cos r\cos h-\sin r\sin p\sin h & -\sin r\cos p & \cos r\sin h+\sin r\sin p\cos h\\\sin r\cos h+\cos r\sin p\sin h & \cos r\cos p & \sin r\sin h-\cos r\sin p\cos h\\-\cos p\sin h & \sin p & \cos p\cos h\end{bmatrix}
= ⎣ ⎢ ⎡ cos r cos h − sin r sin p sin h sin r cos h + cos r sin p sin h − cos p sin h − sin r cos p cos r cos p sin p cos r sin h + sin r sin p cos h sin r sin h − cos r sin p cos h cos p cos h ⎦ ⎥ ⎤
∴ e 21 = sin p , e 01 e 11 = − sin r cos r = − tan r , e 20 e 22 = − sin h cos h = − tan h \therefore e_{21}=\sin p,\;\;\;\frac{e_{01}}{e_{11}}=\frac{-\sin r}{\cos r}=-\tan r,\;\;\;\frac{e_{20}}{e_{22}}=\frac{-\sin h}{\cos h}=-\tan h
∴ e 2 1 = sin p , e 1 1 e 0 1 = cos r − sin r = − tan r , e 2 2 e 2 0 = cos h − sin h = − tan h
∴ h = arctan ( − e 20 e 22 ) = atan2 ( − e 20 , e 22 ) p = arcsin ( e 21 ) r = arctan ( − e 01 e 11 ) = atan2 ( − e 01 , e 11 ) \therefore \begin{matrix}h=\arctan(-\frac{e_{20}}{e_{22}})=\text{atan2}(-e_{20},e_{22})\\p=\arcsin(e_{21})\\r=\arctan(-\frac{e_{01}}{e_{11}})=\text{atan2}(-e_{01},e_{11})\end{matrix}
∴ h = arctan ( − e 2 2 e 2 0 ) = atan2 ( − e 2 0 , e 2 2 ) p = arcsin ( e 2 1 ) r = arctan ( − e 1 1 e 0 1 ) = atan2 ( − e 0 1 , e 1 1 )
上述推导还可能遇到cos p = 0 \cos p=0 cos p = 0 万向锁 gimbal lock 该视频 )。在这种情况下,r的值决定了在这个轴上的最终旋转。因此,我们将h设为0,则:
E = [ cos r sin r cos p sin r sin p sin r cos r cos p − cos r sin p 0 sin p cos p ] \mathbf{E}=\begin{bmatrix}\cos r & \sin r\cos p & \sin r\sin p\\\sin r & \cos r\cos p & -\cos r\sin p\\0 & \sin p & \cos p\end{bmatrix}
E = ⎣ ⎢ ⎡ cos r sin r 0 sin r cos p cos r cos p sin p sin r sin p − cos r sin p cos p ⎦ ⎥ ⎤
∴ e 10 e 00 = sin r cos r = tan r \therefore \frac{e_{10}}{e_{00}}=\frac{\sin r}{\cos r}=\tan r
∴ e 0 0 e 1 0 = cos r sin r = tan r
∴ r = atan2 ( e 10 , e 00 ) \therefore r=\text{atan2}(e_{10},e_{00})
∴ r = atan2 ( e 1 0 , e 0 0 )
需要注意的是,由于p = arcsin ( e 21 ) p=\text{arcsin}(e_{21}) p = arcsin ( e 2 1 ) − π / 2 ≤ p ≤ π / 2 -\pi/2\leq p \leq \pi/2 − π / 2 ≤ p ≤ π / 2 E 的时候p的值不在这个范围内,那根据上述步骤得到的p肯定和实际的p不一样。这也就意味着不止一组r、p、h可以得到同样的欧拉变换。
尽管欧拉角存在万向锁这种无法避免的问题,它依然被广泛使用,因为它在使用动画曲线编辑器时很好用。
前面的例子都是假设我们已经知道物体经过了哪些变换得到了最终的变换矩阵。但实际运用时我们往往不知道中间经过了哪些步骤,这就需要分解矩阵。
平移矩阵可以直接通过变换矩阵的最后一列获取;计算行列式的正负可以判断是否发生了反射;旋转、缩放和剪切不是这么直观就能分解出来的,但是也有一些固定的方法,但本文不再讲述。
假设我们需要将物体绕r 轴旋转ɑ度,我们需要先对物体进行M 变换,使其本地空间的x轴和r 轴对齐,将其旋转后再进行M -1 变换,如下图所示。
通过观察我们可以得知:
s = { ( 0 , − r z , r y ) if ∣ r x ∣ ≤ ∣ r y ∣ and ∣ r x ∣ ≤ ∣ r z ∣ ( − r z , 0 , r x ) if ∣ r y ∣ ≤ ∣ r x ∣ and ∣ r y ∣ ≤ ∣ r z ∣ ( − r y , r x , 0 ) if ∣ r z ∣ ≤ ∣ r x ∣ and ∣ r z ∣ ≤ ∣ r y ∣ \mathbf{s}=\begin{cases}
(0,-r_z,r_y) &\text{ if } |r_x| \leq |r_y| \;\;\;\text{and}\;\;\; |r_x| \leq |r_z| \\
(-r_z,0,r_x) &\text{ if } |r_y| \leq |r_x| \;\;\;\text{and}\;\;\; |r_y| \leq |r_z| \\
(-r_y,r_x,0) &\text{ if } |r_z| \leq |r_x| \;\;\;\text{and}\;\;\; |r_z| \leq |r_y|
\end{cases} s = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ( 0 , − r z , r y ) ( − r z , 0 , r x ) ( − r y , r x , 0 ) if ∣ r x ∣ ≤ ∣ r y ∣ and ∣ r x ∣ ≤ ∣ r z ∣ if ∣ r y ∣ ≤ ∣ r x ∣ and ∣ r y ∣ ≤ ∣ r z ∣ if ∣ r z ∣ ≤ ∣ r x ∣ and ∣ r z ∣ ≤ ∣ r y ∣
将s 和r normalize之后,t = s × r \mathbf{t}=\mathbf{s} \times \mathbf{r} t = s × r s 的分支步骤。将r 、s 、t 和x、y、z轴对齐的转换矩阵为:
M = [ r T s T t T ] \mathbf{M}=\begin{bmatrix}\mathbf{r}^T\\\mathbf{s}^T\\\mathbf{t}^T\end{bmatrix}
M = ⎣ ⎢ ⎡ r T s T t T ⎦ ⎥ ⎤
最终用来进行转换的矩阵为:
X = M T R x ( α ) M \mathbf{X}=\mathbf{M}^T\mathbf{R}_x(\alpha)\mathbf{M}
X = M T R x ( α ) M
还有另外一个直接进行旋转变换的公式将不做推导,直接给出,如下:
R = [ cos ϕ + ( 1 − cos ϕ ) r x 2 ( 1 − cos ϕ ) r x r y − r z sin ϕ ( 1 − cos ϕ ) r x r z + r y sin ϕ ( 1 − cos ϕ ) r x r y + r z sin ϕ cos ϕ + ( 1 − cos ϕ ) r y 2 ( 1 − cos ϕ ) r y r z − r x sin ϕ ( 1 − cos ϕ ) r x r z − r y sin ϕ ( 1 − cos ϕ ) r y r z + r x sin ϕ cos ϕ + ( 1 − cos ϕ ) r z 2 ] \tiny{
\mathbf{R}=\\
\begin{bmatrix}
\cos \phi+(1-\cos \phi)r_x^2 & (1-\cos \phi)r_xr_y-r_z\sin \phi & (1-\cos \phi)r_xr_z+r_y\sin \phi\\
(1-\cos \phi)r_xr_y+r_z\sin \phi & \cos \phi+(1-\cos \phi)r_y^2 & (1-\cos \phi)r_yr_z-r_x\sin \phi\\
(1-\cos \phi)r_xr_z-r_y\sin \phi & (1-\cos \phi)r_yr_z+r_x\sin \phi & \cos \phi+(1-\cos \phi)r_z^2
\end{bmatrix}
} R = [ cos ϕ + ( 1 − cos ϕ ) r x 2 ( 1 − cos ϕ ) r x r y + r z sin ϕ ( 1 − cos ϕ ) r x r z − r y sin ϕ ( 1 − cos ϕ ) r x r y − r z sin ϕ cos ϕ + ( 1 − cos ϕ ) r y 2 ( 1 − cos ϕ ) r y r z + r x sin ϕ ( 1 − cos ϕ ) r x r z + r y sin ϕ ( 1 − cos ϕ ) r y r z − r x sin ϕ cos ϕ + ( 1 − cos ϕ ) r z 2 ]
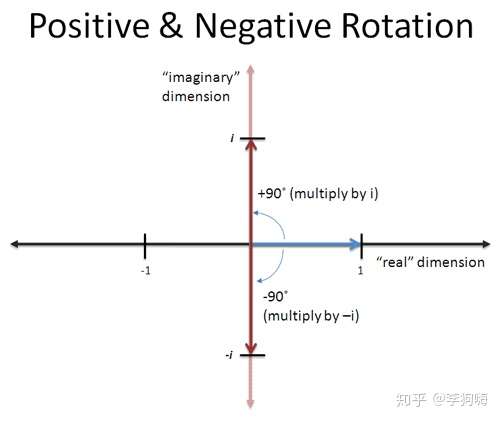
虚数(imaginary number):通俗表示为i = − 1 i=\sqrt{-1} i = − 1 i 2 i^2 i 2 1 × i × i = − 1 1\times i \times i=-1 1 × i × i = − 1 Z = a + b i Z=a+bi Z = a + b i
我们将四元数q ^ \hat{\mathbf{q}} q ^
q ^ = ( q v , q w ) = i q x + j q y + k q z + q w = q v + q w \hat{\mathbf{q}}=(\mathbf{q}_v,q_w)=iq_x+jq_y+kq_z+q_w=\mathbf{q}_v+q_w
q ^ = ( q v , q w ) = i q x + j q y + k q z + q w = q v + q w
q v = i q x + j q y + k q z = ( q x , q y , q z ) \mathbf{q}_v=iq_x+jq_y+kq_z=(q_x,q_y,q_z)
q v = i q x + j q y + k q z = ( q x , q y , q z )
i 2 = j 2 = k 2 = − 1 , j k = − k j = i , k i = − i k = j , j i = − j i = k i^2=j^2=k^2=-1,jk=-kj=i,ki=-ik=j,ji=-ji=k
i 2 = j 2 = k 2 = − 1 , j k = − k j = i , k i = − i k = j , j i = − j i = k
其中,q w q_w q w q ^ \hat{\mathbf{q}} q ^ q v \mathbf{q}_v q v q v \mathbf{q}_v q v q ^ , r ^ \hat{\mathbf{q}},\hat{\mathbf{r}} q ^ , r ^
q ^ r ^ = ( i q x + j q y + k q z + q w ) ( i r x + j r y + k r z + r w ) \hat{\mathbf{q}}\hat{\mathbf{r}}=(iq_x+jq_y+kq_z+q_w)(ir_x+jr_y+kr_z+r_w)
q ^ r ^ = ( i q x + j q y + k q z + q w ) ( i r x + j r y + k r z + r w )
= i ( q y r z − q z r y + r w q x + q w r x ) =i(q_yr_z-q_zr_y+r_wq_x+q_wr_x)
= i ( q y r z − q z r y + r w q x + q w r x )
+ j ( q z r x − q x r z + r w q y + q w r y ) +j(q_zr_x-q_xr_z+r_wq_y+q_wr_y)
+ j ( q z r x − q x r z + r w q y + q w r y )
+ k ( q x r y − q y r x + r w q z + q w r z ) +k(q_xr_y-q_yr_x+r_wq_z+q_wr_z)
+ k ( q x r y − q y r x + r w q z + q w r z )
+ q w r w − q x r x − q y r y − q z r z +q_wr_w-q_xr_x-q_yr_y-q_zr_z
+ q w r w − q x r x − q y r y − q z r z
= ( q v × r v + r w q v + q w r v , q w r w − q v ⋅ r v ) =(\mathbf{q}_v\times \mathbf{r}_v+r_w\mathbf{q}_v+q_w\mathbf{r}_v,q_wr_w-\mathbf{q}_v\cdot\mathbf{r}_v)
= ( q v × r v + r w q v + q w r v , q w r w − q v ⋅ r v )
其加法(addition)、共轭(conjugate)、模(norm)、恒等式(Identity)分别为:
Addition: q ^ + r ^ = ( q v , q w ) + ( r v , r w ) = ( q v + r v , q w + r w ) \textbf{Addition:}\;\;\;\hat{\mathbf{q}}+\hat{\mathbf{r}}=(\mathbf{q}_v,q_w)+(\mathbf{r}_v,r_w)=(\mathbf{q}_v+\mathbf{r}_v,q_w+r_w)
Addition: q ^ + r ^ = ( q v , q w ) + ( r v , r w ) = ( q v + r v , q w + r w )
Conjugate: q ^ ∗ = ( q v , q w ) ∗ = ( − q v , q w ) \textbf{Conjugate:}\;\;\;\hat{\mathbf{q}}^*=(\mathbf{q}_v,q_w)^*=(-\mathbf{q}_v,q_w)
Conjugate: q ^ ∗ = ( q v , q w ) ∗ = ( − q v , q w )
Norm: n ( q ^ ) = ∥ q ^ ∥ = q ^ q ^ ∗ = q ^ ∗ q ^ = q v ⋅ q v + q w 2 \textbf{Norm:}\;\;\;n(\hat{\mathbf{q}})=\|\hat{\mathbf{q}}\|=\sqrt{\hat{\mathbf{q}}\hat{\mathbf{q}}^*}=\sqrt{\hat{\mathbf{q}}^*\hat{\mathbf{q}}}=\sqrt{\mathbf{q}_v\cdot \mathbf{q}_v+q_w^2}
Norm: n ( q ^ ) = ∥ q ^ ∥ = q ^ q ^ ∗ = q ^ ∗ q ^ = q v ⋅ q v + q w 2
= q x 2 + q y 2 + q z 2 + q w 2 =\sqrt{q_x^2+q_y^2+q_z^2+q_w^2}
= q x 2 + q y 2 + q z 2 + q w 2
Identity: i ^ = ( 0 , 1 ) \textbf{Identity:}\;\;\;\hat{\mathbf{i}}=(\mathbf{0},1)
Identity: i ^ = ( 0 , 1 )
由于q ^ − 1 q ^ = q ^ q ^ − 1 = 1 \hat{\mathbf{q}}^{-1}\hat{\mathbf{q}}=\hat{\mathbf{q}}\hat{\mathbf{q}}^{-1}=1 q ^ − 1 q ^ = q ^ q ^ − 1 = 1
q ^ − 1 = 1 q ^ = 1 ∥ q ^ ∥ 2 q ^ ∗ \hat{\mathbf{q}}^{-1}=\frac{1}{\hat{\mathbf{q}}}=\frac{1}{\|\hat{\mathbf{q}}\|^2}\hat{\mathbf{q}}^*
q ^ − 1 = q ^ 1 = ∥ q ^ ∥ 2 1 q ^ ∗
四元数乘以一个实数的运算和顺序无关,即:
s q ^ = q ^ s = ( s q v , s q w ) s\hat{\mathbf{q}}=\hat{\mathbf{q}}s=(s\mathbf{q}_v,sq_w)
s q ^ = q ^ s = ( s q v , s q w )
单位四元数(unit quaternion)即∥ q ^ ∥ = 1 \|\hat{\mathbf{q}}\|=1 ∥ q ^ ∥ = 1
Z = i sin ϕ + cos ϕ = e i ϕ \mathbf{Z}=i\sin \phi+\cos \phi=e^{i\phi}
Z = i sin ϕ + cos ϕ = e i ϕ
我们知道d d x e i x = i e i x \frac{d}{d_x}e^{ix}=ie^{ix} d x d e i x = i e i x f ( x ) = e x f(x)=e^x f ( x ) = e x f ( x ) = e i x f(x)=e^{ix} f ( x ) = e i x Z = f ( x ) = i sin x + cos x Z=f(x)=i\sin x+\cos x Z = f ( x ) = i sin x + cos x d d x f ( x ) = i f ( x ) \frac{d}{d_x}f(x)=if(x) d x d f ( x ) = i f ( x ) f ( x ) = e i x f(x)=e^{ix} f ( x ) = e i x
类似的,四元数也能表示为:
q ^ = ( sin ϕ u q , cos ϕ ) = sin ϕ u q + cos ϕ \hat{\mathbf{q}}=(\sin \phi \mathbf{u}_q,\cos \phi)=\sin \phi \mathbf{u}_q+\cos \phi
q ^ = ( sin ϕ u q , cos ϕ ) = sin ϕ u q + cos ϕ
其中,u q \mathbf{u}_q u q ∥ u q ∥ = 1 \|\mathbf{u}_q\|=1 ∥ u q ∥ = 1
我们可以很方便地用单位四元数来表示物体在三维空间的旋转。假设现在有一个点或向量p = [ p x p y p z p w ] T \mathbf{p}=\begin{bmatrix}p_x & p_y & p_z & p_w\end{bmatrix}^T p = [ p x p y p z p w ] T p ^ \hat{\mathbf{p}} p ^ q ^ = ( sin ϕ u q , cos ϕ ) \hat{\mathbf{q}}=(\sin \phi \mathbf{u}_q,\cos \phi) q ^ = ( sin ϕ u q , cos ϕ ) q ^ p ^ q ^ − 1 \hat{\mathbf{q}}\hat{\mathbf{p}}\hat{\mathbf{q}}^{-1} q ^ p ^ q ^ − 1 p ^ \hat{\mathbf{p}} p ^ p 沿着u q \mathbf{u}_q u q 2 ϕ 2\phi 2 ϕ q ^ \hat{\mathbf{q}} q ^ ∥ q ∥ = 1 \|q\|=1 ∥ q ∥ = 1 q ^ − 1 = q ^ ∗ \hat{\mathbf{q}}^{-1}=\hat{\mathbf{q}}^* q ^ − 1 = q ^ ∗
给定两个单位四元数q ^ , r ^ \hat{\mathbf{q}},\hat{\mathbf{r}} q ^ , r ^ p 先按q ^ \hat{\mathbf{q}} q ^ r ^ \hat{\mathbf{r}} r ^
r ^ ( q ^ p ^ q ^ ∗ ) r ^ ∗ = ( r ^ q ^ ) p ^ ( r ^ q ^ ) ∗ = c ^ p ^ c ^ ∗ \hat{\mathbf{r}}(\hat{\mathbf{q}}\hat{\mathbf{p}}\hat{\mathbf{q}}^*)\hat{\mathbf{r}}^*=(\hat{\mathbf{r}}\hat{\mathbf{q}})\hat{\mathbf{p}}(\hat{\mathbf{r}}\hat{\mathbf{q}})^*=\hat{\mathbf{c}}\hat{\mathbf{p}}\hat{\mathbf{c}}^*
r ^ ( q ^ p ^ q ^ ∗ ) r ^ ∗ = ( r ^ q ^ ) p ^ ( r ^ q ^ ) ∗ = c ^ p ^ c ^ ∗
其中,c ^ = r ^ q ^ \hat{\mathbf{c}}=\hat{\mathbf{r}}\hat{\mathbf{q}} c ^ = r ^ q ^
本段后续内容都是对于各种变换的计算公式,由于这些在软件或游戏引擎的底层中都已经实现,我们大概了解原理即可,具体推导过程省略。
假如现在有一支机械臂,它的动画由上臂和前臂组成。如果这个动画通过刚体变换来实现,就显得不是那么真实,因为关节包含了上臂和前臂重叠的部分。更好的实现方式是将整个机械臂当成一个物体来处理。
Vertex Blending又称为线性混合蒙皮(linear-blend skinning)、包络(enveloping)或骨骼子空间变形(skeleton-subspace deformation)。简单来说,在上述例子中,前臂和上臂各自使用单独的动画,但是在关节处通过一个拥有弹性的部位相连。这个部位有一部分顶点受上臂的变换矩阵影响,有一部分顶点受前臂的变换矩阵影响。在此基础上,同一个顶点就可以受到多个变换矩阵的影响,最终将不同权重的变换矩阵结果混合起来。这种用户自定义某个顶点受哪些骨骼影响的权重的操作就是所谓的“刷权重”。一个顶点p 随着时间t变换的坐标可以表示为:
u ( t ) = ∑ i = 0 n − 1 w i B i ( t ) M i − 1 p \mathbf{u}(t)=\sum_{i=0}^{n-1}w_i\mathbf{B}_i(t)\mathbf{M}_i^{-1}\mathbf{p}
u ( t ) = i = 0 ∑ n − 1 w i B i ( t ) M i − 1 p
其中,n为所有骨骼的数量,w i w_i w i p 的权重。M i \mathbf{M}_i M i B i ( t ) \mathbf{B}_i(t) B i ( t )
Vertex Blending很适合在GPU上使用。网格中的顶点可以存储在GPU的静态缓冲区,每一帧只需要传入骨骼的变换矩阵,就能通过顶点着色器计算出所有顶点所受的影响,这样可以有效降低CPU和GPU之间的数据传输,提高GPU渲染效率。骨骼变换的信息也可以存储在贴图中,以防寄存器存储达到上限。
在一些特殊的算法,比如下一节的变形目标(morph targets)中,所有的权重加起来也可以不为1。
线性的Vertex Blending算法的缺点是容易产生不必要的折叠(folding)、扭曲(twisting)和子相交(self-intersection),如下图所示。
更好的办法是使用对偶四元数 dual quaternions 旋转中心蒙皮 center-of-rotation skinning
局部变换应该是刚体变换
拥有相似权重的顶点应该具有相似的变换
每个顶点的旋转中心都是预先计算好的,正交(刚体)约束则用来防止弯头坍塌和糖纸扭曲。在运行时,该算法类似于linear blend skinning,旋转中心由GPU执行linear blend skinning,然后执行四元数混合步骤。
目前最常用的算法似乎还是Linear Blend Skinning(LBS)。Center-of-Rotation Skinning(CoRS)出自Disney的一篇论文 ,从其展示的效果和效率来看,似乎是目前效果最好、效率相对较高的算法。
简单来说就是在时间点t0和t1分别有两个不同的三维模型,通过某种插值算法在两个时间点内的每个时间点都能获得一个模型。
Morphing主要需要解决两个问题,一个是顶点对应(vertex correspondence) 插值(interpolation)
如果两个模型已经拥有一对一的顶点关系,那就可以很容易地对每个顶点进行插值(比如线性插值)。
有一种变形方式叫做变形目标(morph targets)或
在上图中,我们有一张中性的脸的模型,记作N \mathcal{N} N k ≥ 1 k\geq 1 k ≥ 1 P i , i ∈ [ 1 , … , k ] \mathcal{P}_i,i\in [1,…,k] P i , i ∈ [ 1 , … , k ] D i = P i − N \mathcal{D}_i=\mathcal{P}_i-\mathcal{N} D i = P i − N
M = N + ∑ i = 1 k w i D i \mathcal{M}=\mathcal{N}+\sum_{i=1}^{k}w_i\mathcal{D}_i
M = N + i = 1 ∑ k w i D i
其中w i w_i w i
Morph targets是动画中很有用的一项技术,因为用户可以独立控制每个不同的动画特征。pose-space deformation技术可以将vertex blending和morph targets结合起来。还可以使用贴图来存储和读取动画的切换。支持stream-out和每个顶点ID的硬件允许单个模型使用更多数量的变形目标,并且可以专门在GPU上进行计算。使用低分辨率的网格、在曲面细分阶段生成更多顶点并使用位移贴图 displacement texture
在剪辑场景中,可能需要使用高质量的动画,这种变形用上面的算法无法表示出来。一个很自然的做法是将每一帧所有的顶点数据存储在本地磁盘,实时读取这些数据来更新网格。但是对于一段短动画中一个简单的30000个顶点的模型,这些数据的传输量就能达到50MB/s。有一些方法可以将内存消耗降低到10%左右。
首先,使用量化 quantization 空间 spatial 时间 temporal 四边形预测 parallelogram prediction
在本章前面提到的变换都没有涉及第四个坐标w分量,在变换后,点还是点,向量还是向量,4x4矩阵的最后一行依然是[0 0 0 1]。透视投影矩阵 Perspective Projection Matrices 正交投影 Orthographic Projection
在本节中,我们默认观察者的视线是沿着z轴的负方向,上方为y轴,右手为x轴。
正交投影的一个特征是平行线投影完依然是平行线。不管物体距离相机多远,它的大小都不变,它的变换矩阵可以表示为:
P o = [ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 ] \mathbf{P}_o=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} P o = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
由于∥ P o ∥ = 0 \|\mathbf{P}_o\|=0 ∥ P o ∥ = 0 P o \mathbf{P}_o P o
另一种更常用的正交投影矩阵可以表示为[ l , r , b , t , n , f ] [l, r, b, t, n, f] [ l , r , b , t , n , f ]
AABB的最小坐标为(l, b, n),最大坐标为(r, t, f)。由于观察者是看向z轴负方向,因此n>f。在OpenGL中,变换后的轴对齐立方体的最小坐标为(-1, -1, -1),最大坐标为(1, 1, 1)。在DirectX中两者则是(-1, -1, 0)和(1, 1, 1)。这个立方体就是第二章中提到的规范视域体(canonical view volume) 标准化设备坐标(Normalized Device Coordinate, NDC)
完整的投影变换可以表示为:
P o = S ( s ) T ( t ) = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 f − n 0 0 0 0 1 ] [ 1 0 0 − r + l 2 0 1 0 − t + b 2 0 0 1 − f + n 2 0 0 0 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 2 f − n − f + n f − n 0 0 0 1 ] \mathbf{P}_o=\mathbf{S}(\mathbf{s})\mathbf{T}(\mathbf{t})\\
=\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & 0\\
0 & \frac{2}{t-b} & 0 & 0\\
0 & 0 & \frac{2}{f-n} & 0\\
0 & 0 & 0 & 1
\end{bmatrix}\begin{bmatrix}
1 & 0 & 0 & -\frac{r+l}{2}\\
0 & 1 & 0 & -\frac{t+b}{2}\\
0 & 0 & 1 & -\frac{f+n}{2}\\
0 & 0 & 0 & 1
\end{bmatrix}\\
=\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{2}{f-n} & -\frac{f+n}{f-n}\\
0 & 0 & 0 & 1
\end{bmatrix} P o = S ( s ) T ( t ) = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 0 0 0 0 t − b 2 0 0 0 0 f − n 2 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 0 − 2 r + l − 2 t + b − 2 f + n 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 0 0 0 0 t − b 2 0 0 0 0 f − n 2 0 − r − l r + l − t − b t + b − f − n f + n 1 ⎦ ⎥ ⎥ ⎥ ⎤
其中,s = ( 2 / ( r − l ) , 2 / ( t − b ) , 2 / ( f − n ) ) , t = ( − ( r + l ) / 2 , − ( t + b ) / 2 , − ( f + n ) / 2 ) \mathbf{s}=(2/(r-l),2/(t-b),2/(f-n)),\mathbf{t}=(-(r+l)/2,-(t+b)/2,-(f+n)/2) s = ( 2 / ( r − l ) , 2 / ( t − b ) , 2 / ( f − n ) ) , t = ( − ( r + l ) / 2 , − ( t + b ) / 2 , − ( f + n ) / 2 ) P o \mathbf{P}_o P o P o − 1 = T ( − t ) S ( ( r − l ) / 2 , ( t − b ) / 2 , ( f − n ) / 2 ) \mathbf{P}_o^{-1}=\mathbf{T}(-t)\mathbf{S}((r-l)/2,(t-b)/2,(f-n)/2) P o − 1 = T ( − t ) S ( ( r − l ) / 2 , ( t − b ) / 2 , ( f − n ) / 2 )
在计算机图形学中,投影后通常使用左手坐标系。假设AABB和变换后的规范视域体一样大小,也即(l, b, n)和(r, t, f)分别为(-1, -1, 1)和(1, 1, -1),带入上面的公式可得:
P o = [ 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 1 ] \mathbf{P}_o=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & -1 & 0\\
0 & 0 & 0 & 1
\end{bmatrix} P o = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 − 1 0 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎤
这个矩阵也就是从右手坐标系变换到左手坐标系的镜像矩阵。
DirectX中的z-depth范围是[0,1],而不是OpenGL中的[-1,1]。因此,我们可以在P o \mathbf{P}_o P o
M s t = [ 1 0 0 0 0 1 0 0 0 0 0.5 0 0 0 1 ] \mathbf{M}_{st}=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & & 0.5\\
0 & 0 & 0 & 1
\end{bmatrix} M s t = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 0 0 0 0 . 5 1 ⎦ ⎥ ⎥ ⎥ ⎤
因此,在DirectX中使用的正交矩阵为:
P o [ 0 , 1 ] = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 1 f − n − n f − n 0 0 0 1 ] \mathbf{P}_{o[0,1]}=\begin{bmatrix}
\frac{2}{r-l} & 0 & 0 & -\frac{r+l}{r-l}\\
0 & \frac{2}{t-b} & 0 & -\frac{t+b}{t-b}\\
0 & 0 & \frac{1}{f-n} & -\frac{n}{f-n}\\
0 & 0 & 0 & 1
\end{bmatrix} P o [ 0 , 1 ] = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 0 0 0 0 t − b 2 0 0 0 0 f − n 1 0 − r − l r + l − t − b t + b − f − n n 1 ⎦ ⎥ ⎥ ⎥ ⎤
透视投影(perspective projection) 相比正交投影,透视投影更常见,也更符合真实的视角:越远的物体看起来越小。在透视投影中,平行线会在最远处相交于一点。
现在假设相机在原点,我们要将一个点p 投影到z=-d, d>0的平面,得到一个新的点q = ( q x , q y , − d ) \mathbf{q}=(q_x,q_y,-d) q = ( q x , q y , − d )
q x p x = − d p z ⟺ q x = − d p x p z \frac{q_x}{p_x}=\frac{-d}{p_z} \iff q_x=-d\frac{p_x}{p_z}
p x q x = p z − d ⟺ q x = − d p z p x
q 的另外两个分量分别是q y = − d p y p z , q z = − d q_y=-d\frac{p_y}{p_z},q_z=-d q y = − d p z p y , q z = − d
P p = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 − 1 / d 0 ] \mathbf{P}_p=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & -1/d & 0
\end{bmatrix} P p = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 − 1 / d 0 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎤
因为:
q = P p p = [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 − 1 / d 0 ] [ p x p y p z 1 ] = [ p x p y p z − p z / d ] ⇒ [ − d p x / z − d p y / z − d 1 ] \mathbf{q}=\mathbf{P}_p\mathbf{p}=\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & -1/d & 0
\end{bmatrix}\begin{bmatrix}
p_x\\
p_y\\
p_z\\
1
\end{bmatrix}\\
=\begin{bmatrix}
p_x\\
p_y\\
p_z\\
-p_z/d
\end{bmatrix}\Rightarrow \begin{bmatrix}
-dp_x/_z\\
-dp_y/_z\\
-d\\
1
\end{bmatrix} q = P p p = ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 0 0 0 1 0 0 0 0 1 − 1 / d 0 0 0 0 ⎦ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎡ p x p y p z 1 ⎦ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎡ p x p y p z − p z / d ⎦ ⎥ ⎥ ⎥ ⎤ ⇒ ⎣ ⎢ ⎢ ⎢ ⎡ − d p x / z − d p y / z − d 1 ⎦ ⎥ ⎥ ⎥ ⎤
和正交投影一样,透视投影其实也需要将视锥体投影到规范视域体,而不是投影到一个平面(不可逆)。透视投影的视锥体从z=n开始,到z=f,其中0<n<f。在z=n处的正方体左下角坐标为(l, b, n),右上角为(r, t, n),如下图所示:
参数(l, r, b, t, n, f)决定了相机的视锥体大小。水平面的视域 Field of View, FOV r ≠ − l r\neq -l r = − l t ≠ − b t\neq -b t = − b 不对称视锥 Asymmetric Frusta
FOV是提供场景感的重要因素。和计算机屏幕相比,眼睛本身具有物理的FOV,关系为:
ϕ = 2 arctan ( w / 2 d ) \phi=2\arctan (w/2d)
ϕ = 2 arctan ( w / 2 d )
其中,ϕ \phi ϕ w w w d d d ϕ = 2 arctan ( 36 / ( 2 × 50 ) ) = 39. 6 ∘ \phi=2\arctan (36/(2\times 50))=39.6^{\circ} ϕ = 2 arctan ( 3 6 / ( 2 × 5 0 ) ) = 3 9 . 6 ∘
使用较小的FOV会降低透视效果,而太大的FOV会使物体扭曲,尤其是在屏幕的边缘,还会放大物体的缩放倍数。但是更宽的FOV也有好处,它能让观察者觉得物体更大、更令人印象深刻,因而能让观察者获得周围物体更多的信息。
将视锥体投影到规范视域体的透视变换矩阵为:
P p = [ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 f + n f − n − 2 f n f − n 0 0 1 0 ] \mathbf{P}_{p}=\begin{bmatrix}
\frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\
0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\
0 & 0 & \frac{f+n}{f-n} & -\frac{2fn}{f-n}\\
0 & 0 & 1 & 0
\end{bmatrix} P p = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 n 0 0 0 0 t − b 2 n 0 0 − r − l r + l − t − b t + b f − n f + n 1 0 0 − f − n 2 f n 0 ⎦ ⎥ ⎥ ⎥ ⎤
将其应用于一个点,会得到另一个点q = ( q x , q y , q z , q w ) T \mathbf{q}=(q_x,q_y,q_z,q_w)^T q = ( q x , q y , q z , q w ) T p ,我们需要将其他分量除以w分量,即:
p = ( q x / q w , q y / q w , q z / q w , 1 ) \mathbf{p}=(q_x/q_w,q_y/q_w,q_z/q_w,1)
p = ( q x / q w , q y / q w , q z / q w , 1 )
通过计算可证明,当一个点的z=f时,它投影后的z为1;z=n时,它投影后的z为-1。
当点的z>f时,可知其经过投影后z>1,超出了规范视域体,因此不会被渲染。我们也可以将f设为无穷大,则投影矩阵就变成了:
P p = [ 2 n r − l 0 − r + l r − l 0 0 2 n t − b − t + b t − b 0 0 0 1 − 2 n 0 0 1 0 ] \mathbf{P}_{p}=\begin{bmatrix}
\frac{2n}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\
0 & \frac{2n}{t-b} & -\frac{t+b}{t-b} & 0\\
0 & 0 & 1 & -2n\\
0 & 0 & 1 & 0
\end{bmatrix} P p = ⎣ ⎢ ⎢ ⎢ ⎡ r − l 2 n 0 0 0 0 t − b 2 n 0 0 − r − l r + l − t − b t + b 1 1 0 0 − 2 n 0 ⎦ ⎥ ⎥ ⎥ ⎤
对于OpenGL来说,投影矩阵为:
P OpenGL = [ 2 n ′ r − l 0 r + l r − l 0 0 2 n ′ t − b t + b t − b 0 0 0 − f ′ + n ′ f ′ − n ′ − 2 f ′ n ′ f ′ − n ′ 0 0 − 1 0 ] \mathbf{P}_{\text{OpenGL}}=\begin{bmatrix}
\frac{2n'}{r-l} & 0 & \frac{r+l}{r-l} & 0\\
0 & \frac{2n'}{t-b} & \frac{t+b}{t-b} & 0\\
0 & 0 & -\frac{f'+n'}{f^{'}-n'} & -\frac{2f'n'}{f'-n'}\\
0 & 0 & -1 & 0
\end{bmatrix} P OpenGL = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ r − l 2 n ′ 0 0 0 0 t − b 2 n ′ 0 0 r − l r + l t − b t + b − f ′ − n ′ f ′ + n ′ − 1 0 0 − f ′ − n ′ 2 f ′ n ′ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
更简单的表示方法是使用垂直FOV(ϕ \phi ϕ a = w / h , n ′ , f ′ a=w/h,n',f' a = w / h , n ′ , f ′
P OpenGL = [ c / a 0 0 0 0 c 0 0 0 0 − f ′ + n ′ f ′ − n ′ − 2 f ′ n ′ f ′ − n ′ 0 0 − 1 0 ] \mathbf{P}_{\text{OpenGL}}=\begin{bmatrix}
c/a & 0 & 0 & 0\\
0 & c & 0 & 0\\
0 & 0 & -\frac{f'+n'}{f^{'}-n'} & -\frac{2f'n'}{f'-n'}\\
0 & 0 & -1 & 0
\end{bmatrix} P OpenGL = ⎣ ⎢ ⎢ ⎢ ⎡ c / a 0 0 0 0 c 0 0 0 0 − f ′ − n ′ f ′ + n ′ − 1 0 0 − f ′ − n ′ 2 f ′ n ′ 0 ⎦ ⎥ ⎥ ⎥ ⎤
其中,c = 1 / tan ( ϕ / 2 ) c=1/\tan (\phi /2) c = 1 / tan ( ϕ / 2 )
在DirectX中,由于n=0而非-1且使用左手坐标系,其矩阵为:
P p [ 0 , 1 ] = [ 2 n ′ r − l 0 − r + l r − l 0 0 2 n ′ t − b − t + b t − b 0 0 0 f ′ f ′ − n ′ − f ′ n ′ f ′ − n ′ 0 0 1 0 ] \mathbf{P}_{p[0,1]}=\begin{bmatrix}
\frac{2n'}{r-l} & 0 & -\frac{r+l}{r-l} & 0\\
0 & \frac{2n'}{t-b} & -\frac{t+b}{t-b} & 0\\
0 & 0 & \frac{f'}{f^{'}-n'} & -\frac{f'n'}{f'-n'}\\
0 & 0 & 1 & 0
\end{bmatrix} P p [ 0 , 1 ] = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ r − l 2 n ′ 0 0 0 0 t − b 2 n ′ 0 0 − r − l r + l − t − b t + b f ′ − n ′ f ′ 1 0 0 − f ′ − n ′ f ′ n ′ 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
使用透视变换的一个结果是计算出的深度值和pz并不是线性相关的。如果我们将一个点乘以上面的投影矩阵,可得:
v = P p = [ . . . . . . x p z + y ± p z ] \mathbf{v}=\mathbf{Pp}=\begin{bmatrix}
...\\
...\\
xp_z+y\\
\pm{p_z}
\end{bmatrix} v = P p = ⎣ ⎢ ⎢ ⎢ ⎡ . . . . . . x p z + y ± p z ⎦ ⎥ ⎥ ⎥ ⎤
假设使用OpenGL的标准投影矩阵,则其中:
x = − f ′ + n ′ f ′ − n ′ , y = − 2 f ′ n ′ f ′ − n ′ x=-\frac{f'+n'}{f'-n'},y=\frac{-2f'n'}{f'-n'}
x = − f ′ − n ′ f ′ + n ′ , y = f ′ − n ′ − 2 f ′ n ′
所得点的深度值为:
z NDC = x p z + y − p z = − ( x + y p z ) z_{\text{NDC}}=\frac{xp_z+y}{-p_z}=-(x+\frac{y}{p_z})
z NDC = − p z x p z + y = − ( x + p z y )
显然,深度值和z值成反比。假如n’=10,f’=110,当p z = 60 p_z=60 p z = 6 0
从图中也能看到,离f较近的一段z坐标,仅对应了较少的深度值区域,尤其是当n越小时,情况越明显。如上图中的蓝色实现,n=1时,z=[0,20]对应了约[-1,0.9]的深度值,z=[20,100]对应了约[0.9,1]的深度值,这样不平均的分布显然会降低深度值的精确度。为了提高其精度,常用的一种方法叫做反向Z reversed z NDC 。下图是几种存储深度值方式的区别(以DirectX为例,zNDC 在0到1之间):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
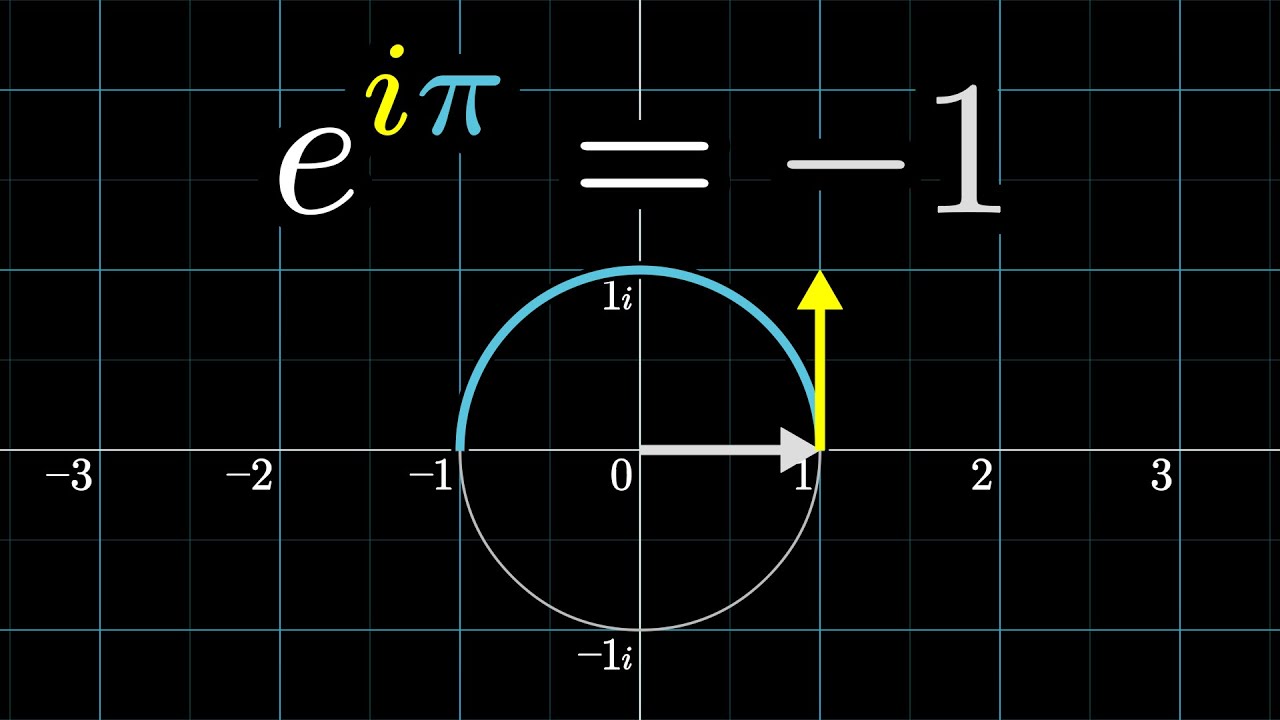
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()